"The role of axioms is to define the boundaries of a theory. It is supposed that within these limits, the theory works. Out of these limits the result is not guaranteed. Thus, in order to understand OTSM, it is necessary to know its axioms".
This material was developed by Nikolai Khomenko and Roland de Guio and finally completed by Roland de Guio (2015).
Edited by I.Kaikov, O. Kaikov.
Introduction
TRIZ is a Russian acronym for "Теория Решения Изобретательских Задач" that holds for "Theory of Inventive Problem Solving". Contrary to the random traditional trial and error, which is based on a highly diverging solution search, TRIZ helps to solve technical problems with a guided heuristic process. This well manageable step by step process aims at developing satisfactory solutions to Non Typical Problems in the specific context of a given problematic situation. The methods and tools are mainly devoted to technical objects, even if the range of the objects may vary from a very simple part to a very complex system. It should be noted that with mentioning TRIZ there are two different aspects: firstly, TRIZ as a theory and, secondly, as methods and tools in the context of its practical applications. In this paper, only the tools built on TRIZ theoretical basis and the performances of which has been enough evaluated to provide evidence of their quality are meant under the word „TRIZ“.
In the seventies, when the effectiveness of TRIZ became indubitable, the idea to extend TRIZ to non-technical domain arose [2]. In the middle of the 80’s, Altshuller, who is the founder of TRIZ, stimulated the development of TRIZ-based theory aimed at solving non-technical problems [3]. The acronym of this theory is OTSM, which holds for «Общая Теория Сильного Мышления» and can be translated as “General Theory of Powerful Thinking”.
Thus, it was said that TRIZ should outgrow into the General Theory of Powerful Thinking (OTSM), that a basis for a universal theory of problem solving should be created. A contradiction, which prevents the creation of a universal instrument for the analysis and solution of problems, was found:
In order to be universal, the rules of problem solving methods should be as general as possible. But the more general the rules of problem solving are, the more general and the less of practical use the solution will be.
And vice versa: when the rules (and methods) are specific and precise, they are helpful for solving a specific problem which is of practical use. However, the more specific they are the less universal they are as well [4][1].
Like any theory, the limits and the basis of OTSM should be defined. With these intentions, Nikolai Khomenko developed a system of axioms for OTSM. This system was coordinated with Altshuller in 1997. In this paper the present stage of OTSM is described, which will evolve. Thus, at the moment of the article's editing, the second and third generations of OTSM tools should already be mentioned. These tools are built on the same basis as the first generation of OTSM tools. These tools are tested in practice in various areas [9].

Figure 1: General scheme of OTSM-TRIZ.
Source : ([5], Khomenko, 1998).
Following paragraphs provide more details about OTSM axioms. They describe the OTSM system of axioms, the four problem solving technologies and their main tools and methods.
1. OTSM system of axioms[2]
In order to use a theory effectively, it is necessary to know the grounding hypothesis of the theory. The knowledge of these foundations and limits make it possible to control the application of the theory. In science, the foundation and limits generally take the shape of axioms.
Let's take the example of two geometries: the geometry of Euclid and the geometry of Lobatchevski. By modifying only one postulate of Euclid’s geometry, Lobatchevski initiated the development of a new geometry, known as the “hyperbolic geometry”. Describing and defining the area of application of a theory is one of the functions of a system of axioms.
The AED dictionary proposes as definition for the word axiom:
“An axiom (logic) is a proposition that is not susceptible of proof or disproof; its truth is assumed to be self-evident”.
The “Grand dictionnaire de la langue Française” completes the definition (translated):
“An axiom is a grounding assertion, the truth accepted without demonstration and on which science and reasoning are based, the conclusions of which are applicable”.
Sometimes, axioms seem to be incredible or lead to many debates. Nevertheless, it does not prevent the development of the theory, even if disagreements can give birth to other theories which may be more adapted to reality.
As explained in the introduction, the role of axioms is to define the boundaries of a theory. It is supposed that within these limits, the theory works. Out of these limits the result is not guaranteed. Thus, in order to understand OTSM, it is necessary to know its axioms.
Misunderstanding or refusal of the axioms would inevitably reduce the efficiency of OTSM application. Moreover it may create a psychological inertia that prevents from building a solution for a problem. In the actual state of OTSM, there are 3 groups of axioms:
- First group – main Axioms: Axiom of description and Axiom of Process (key axioms)
- Second group – Axioms of the thinking process: Axiom of Root of problems, Axiom of Impossibility, Axiom of independent observers (former title of the axiom – Axiom of Reflection)
- Third group – World view axioms: Axiom of Unity, Axiom of Disunity, and Axiom of Connectedness.
1.1. Group 1: Key Axioms of OTSM
The first axiom; the axiom of descriptions (models), is the key axiom and could be the only axiom of OTSM. The other axioms remain in their core a consequence of the axiom of description of models.
Below the borders of OTSM are shown through its system of axioms.
HNN Comment: This is practically impossible Are there any examples that is proved minimal and complete system of Axioms. Usually author is in charge of the system of Axioms. Frankly speaking it is just one axioms – Axiom of models (Descriptions) all others can be viewed as a corollaries from the Axiom of descriptions and 3 postulates of Classical TRZ and Altshuller schema of powerful thinking.
Actually I presented the system of axioms to show scope of the OTSM and its fundamental principles that should be taken into account for developing new tools for solving complex interdisciplinary problematic situations.
1.1.1. Axiom of description (Models)
The first and probably most important axiom has several names: axiom of description, axiom of model or axiom of subjective description of the objective world. The reason for multiple names is the meaning attached to the words in different countries. More often we shall use the term axiom of description which can be formulated in the following way:
There are different ways to describe the world around us. There is an infinite number of ways to describe the world.
All the thoughts about tangible or intangible objects are shaped in our mind as models. But no model is complete because it is built to be used for reaching a given goal (even if this goal is implicit or does not appear to us immediately).
Before presenting the consequences of the axiom of description, it is important to explain the concept of an ideal model of an element. In the framework of OTSM, the ideal model of an element is an absolutely exact description of the element. The ideal model takes into account the past of the element (even its very distant past), its present and its near and distant future. The ideal model is a universal model, which can be applied in any context without any change. Nonetheless, the building of such an ideal model seems unworkable.
Consequences of the axiom of description:
- Any model describes an element only partially, thus limiting the model’s use.
It is important to distinguish a model of an element from the element itself. The recipe is not the dish and the technical drawing of a part is not yet the part. Since any model only partially describes the element, any model is allowed to exist and be employed in the context it was built for.
- In order to compare the efficiency of several models, we have to refer to the goal we want to reach by using these models.
- Any element can be described by an infinite number of models which are different from one another by:
- The level of accuracy of the description (of quantitative characteristics of the element);
- The level of abstraction of the description (of qualitative elements);
- The point of view (it depends, on the one hand, on the objectives that are to be reached with the model and, on the other hand, on the experience and the qualification of the model designer).
- The most accurate description of the element is the element itself.
Indeed, the ideal model, from OTSM’s point of view, is the one that is most complete and true of the element. Due to the partial nature of models, the ideal model of an element could only be the element itself.
- Any initial problem, which is formulated for the first time, is a model of the objective situation described from the point of view of the person who is faced with this problem.
In order to overcome this problematic situation, it is necessary to get off this initial vision and analyze other models of the situation, which are built from other points of view. We suggest adopting at least three or even four points of view:
- The point of view of the person who aims at solving the problem
- The point of view of one or more antagonists of the problem solver
- The point of view of a skilled person in the problem area
- When the problem is concerning a human being, it is necessary to build the model of the problem situation from their point of view (if it is possible) i.e.: from the point of view of the elements from which the problem originates.
- The model is built in order to get answers to a restricted number of questions.
In this context, the ideal model is a model capable to answer any imaginable question about the past, present and future of the element. Let’s repeat that the building of such a model seems impossible, but the concept of the ideal model can be used as a reference in order to evaluate different models.
- Each obtained result can be considered, when being evaluated, both as positive (desirable) and negative (undesirable).
Thus, any solution to a problem induces the apparition of new problems that can be forecasted only partially because they are dependent on the model that is used. Moreover, the connotation or overtone of the result can dramatically change with time. What is today considered as positive can tomorrow become an important problem. Let us illustrate this assertion with the example of the car. During a long period of time, practical aspects of the use of a car were taken into account: speed of moving, autonomy, comfort etc... But today, this vision is changing: pollution, stress during a traffic jam, the enormous increase in the number of cars which leads to parking problems, are criteria that degrade the positive vision of the car. This small example shows how in several decades, the technical solution to the problem “how to move objects and people” loses its positive connotation and gradually is perceived as a problem.
- The design of a model is influenced by several factors that can be either objective (i.e. independent of the person who builds the model) or subjective (i.e. depending on the interests of the person who builds the model).
During the model elaboration, one has to be careful to distinguish objective and subjective factors of the model. One may also try to anticipate the conditions that may change the subjective factors. The last may lead to quite important modifications of the model.
As a consequence of the axiom of description, we can understand why people may not understand each other during a problem solving session. The main reason is that people use different models for the same object. The poem of John Godfrey Saxe (1816-1887) (cf. Appendix I) is a good illustration of this situation.
1.1.2. Axiom of Process
Any element must be seen as a process and vice versa.
This process, which is linked with a human being as soon as we are in a problem solving context, evolves in accordance with objective laws and takes into account a context which appears through objective and subjective factors.
Sometimes we may not feel the evolution, but any element evolves in time, changes its properties even very slowly and so can be compared to a process. Understanding that each element evolves may help to overcome some stereotypes, and progress in the problem analysis. The multi-screen (also known as system operator) is a tool that facilitates this point of view. It will be presented in part 2.
Consequences of the axiom of process:
- It is essential to match solutions with the objective laws that determine the element’s evolution.
This coordination allows modifying the process in order to fit our needs. The better the knowledge about the objective laws, the more capable we are to analyze and solve a problem.
- Ignoring the evolution process and the objective laws may prevent from solving a problem.
- In addition to these objective laws, subjective factors in relation with the problem have to be taken into account (see axiom of the root of the problem).
1.2. Group 2: Axioms of the thinking process
These axioms describe an efficient and effective model of a thinking process for problem solving. They represent the main milestones for building the model of the initial situation and transforming it into a concept of the solution.
There are 4 axioms of the thinking process:
- The axiom of impossibility
- The root of the problem
- The 4 observers of the process
- Axiom of process (everything is process)
1.2.1. Axiom of impossibility
In order to overcome psychological inertia during a problem solving process, it is necessary to accept (temporarily) the assertions, the logical value of which seems “false” at a first glance, and analyze the consequence of these assertions when giving them a logical value “true”.
The problem solving process is a sequential process in the course of which our perception of the problem and, as a consequence, its statement undergo several changes before getting precisely the characteristics of the solution.
Nevertheless, it may sometimes happen that there is no “already-made” solution fitting all the characteristics of the researched solution, and some of the proposed solutions seem unrealistic. In this case there are tools like the “golden fish operator” that allows qualifying the realistic and the unrealistic parts of a solution. Understanding and acceptance of the axiom of impossibility, paired up with the use of the golden fish operator, help to overcome psychological inertia and get access to “unimaginable” feasible solutions. See appendix 2 for more information on the “golden fish operator”.
Consequence of the axiom of impossibility:
- During the problem solving process, it is interesting, and even necessary, to analyze each idea of a solution as soon as it possesses at least one property that may contribute to solving the problem. In OTSM this kind of a solution is called a partial solution. Each on their own, they are unworkable, but by combining them, a workable solution is found most of the time.
- Ideas which prove to be unworkable should not be rejected. They help to build the concept of a solution.
- Possibility or impossibility should not be the only characteristics for analyzing a problem or evaluating a solution. It is also suggested to take into account the following points:
- Objective laws of technical systems’ evolution
- Available resources and context of the real problem situation
- Forecasting of resource and context evolution, including those that seem impossible
In other words, during the problem solving process one must not stick to solutions that seem possible, but dare to explore solutions that at first seem impossible.
1.2.2. Axiom of the root of the problem
Any problem can be stated as a contradiction between our subjective desires for something appearing in a specific context on the one hand, and objective laws that cause this specific situation, one the other hand.
The initial cause of any problem is the contradiction between subjective needs and objective laws. Solving a problem comes down to getting around the objective laws simultaneously respecting them. Knowing the law at the root of the problem helps solving it.
Consequences of the axiom of the root of the problem:
- When facing a problem, the first solving step consists of defining our needs and goals.
- One way to solve the problem may be adapting our needs to the context.
If the subjective needs fit the objective laws that cause the context, then the contradiction is removed and the problem disappears. Of course the contradiction is only removed for a limited amount of time and not in an absolute way.
- When needs cannot be adapted to reality, objective laws at the root of the problem have to be identified.
The knowledge of these laws will allow us to perform an analysis targeting at getting around them. Of course, this analysis requires a deep understanding of these laws.
- For identifying the root of a problem, it is necessary to define the conflicting elements defined above and shape a contradiction between them. Thus, methods for identifying these elements and defining the contradiction are required.
- When facing a problem that seems to have no solution, always start stating the contradictions. It allows one of the following targets:
- finding a typical solution during the formulation of the contradiction
- solving the obtained contradiction with appropriate technologies like OTSM’s technologies
- identifying the missing parts for solving a contradiction without solving it
- It is possible to go around (play with) an objective law only by deep knowledge and understanding of this law.
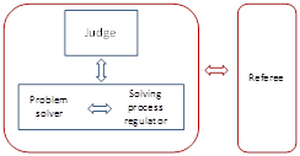
1.2.3. The 4 observers of the problem solving thinking process
Any perceived problem is a transcription of a situation from the point of view of the person who is involved in the problem. In order to overcome the problematic situation; it is necessary to get out of the role of the problem’s “owner” and analyze situation from different points of view.
During the problem solving it is necessary to adopt four points of view:
- The point of view of the problem solver, who is the person directly working on the problem.
The problem solver seeks identifying and understanding the roots of the problem in order to solve it with OTSM tools and methods.
- The point of view of the regulator of OTSM methods’ process.
The regulator verifies that the problem solver respects the OTSM methods’ working rules.
- The point of view of the judge who tries to understand the disagreements between the problem solver and the regulator.
When the problem solver and the regulator disagree, the judge tries to understand their disagreement and helps them to get in harmony.
- The point of view of the referee who tries to understand the world vision of the problem solver, the regulator and the judge when they interact.
The (problem solving) thinking process can be understood as realized by 4 persons, each of them performing a specific function: the problem solver, the regulator, the judge and the referee.
The referee helps to get out of the conflicts that may appear between the solver, the regulator and the judge. In order to reach his goal, the referee looks to the roots of the conflicts, identifies visions (models) of the other three and their stereotypes. Thus, his role consists of understanding to what extent the models differ, and solving the conflicts induced by this difference. The referee is also the one in contact with the sponsor (the silent partner – the one who asked for the problem to be solved) of the problem solving activity.
Above, we presented the solver, the regulator, the judge and the referee as 4 different persons. In practice, one person may play several roles. During OTSM learning for instance, the student plays the role of the solver and the trainer plays the 3 other roles. A good practice of OTSM is necessary when a person has to play all 4 roles.
1.3. Group 3: Axioms of the world views
The art to see objects in a similar way grows on the ability to see them as different and vice versa.
1.3.1. Axiom of unity
The world is a whole and unique system that evolves in accordance with objective laws of all the sub-systems.
The world works as an organism, the parts of which are closely linked. The changes in this organism result from the interaction between its elements, which are constrained by objective laws. They are not the consequence of only the “will” of its elements.
Any change happening in the system induces a set of reactions that spread through the system and affect several elements. Nonetheless, the same change can be interpreted as positive or negative due to the chosen point of view (see axiom of model). This interpretation is also dependent on the part of the world and the period of time that is taken into consideration. What is positive today may be considered as negative a few years later.
1.3.2. Axiom of diversity
The world is a set of different systems, each of them evolving in accordance with its specific laws.
1.3.3. Axiom of coherence (between unity and diversity)
Unity and diversity of the world are governed by the resources used by the different systems. Any resource is subject to general laws and in the same time each resource has its own properties defined by the specific laws of the resource.
Summary of OTSM grounding hypotheses
|
G1 Axioms of description (Key axioms of OTSM) There is an infinite number of ways for described an element Any element must be seen as a process and vice versa |
|
|
G2 Thinking process axioms’ |
G3.World views axioms’ |
|
2.1 Impossibility Accept to work in a concept space where logical values of assertion are unknown, and accept to think them as true temporarily. If necessary qualify what is presently feasible or unfeasible; known or unknown |
3.1+3.2 Unity and diversity The world is both a unique system (unity) and a set of different systems (diversity). |
|
2.2 Root of the problem Contradiction between subjective desires and objective laws. |
|
|
2.3 The 4 observers of the thinking process «Control problem solving process » by 4 roles : Solver(problem owner)-Process regulator-Judge – Referee
|
3.3 Link between unity and diversity governed : resources The world and its sub-systems evolve in accordance with the resources they use.
|
References
1. Altshuller, G. (1979). Tvorchestvo kak tochnaia nauka. Moskva, Sovetskoe radio.
2. Altshuller, G., Filkovski, G. (1975). Sovremennoye sostoyanie TRIZ / http://www.altshuller.ru/triz/triz2.asp
3. Altshuller, G. (1986). .Istoria razvitia ARIZ. http://www.altshuller.ru/triz/ariz-about1.asp
4. Khomenko, N., Super-short introduction into Classical TRIZ and OTSM (2005). http://otsm-triz.org/en/content/super_short_intr_en
5. Khomenko, N. (1998). Fragmenty universal'nogo modul'nogo posobija po OTSM-TRIZ.
6. Khomenko, N. (2005). OTSM Axiom System.
7. Khomenko, N. and Kucharavy, D. (2002). OTSM-TRIZ Problem Solving Process: Solutions and Their Classification. TRIZ-Future, Strasbourg.
8. Kucharavy, D. (2003). TRIZ: techniques. Basic knowledge and skills. Cours.
9. Khomenko, N. (2010), General Theory of Powerful Thinking. OTSM-TRIZ Introductory Seminar. September, 8th, 2010. http://www.osaka-gu.ac.jp/php/nakagawa/TRIZ/eTRIZ/epapers/e2011Papers/eKhomenkoOTSMSeminar2010/eOTSM_Japan_2010_Seminar-100905B.pdf
Annexe I : The Blind Men and the Elephant[3]
It was six men of Indostan
To learning much inclined,
Who went to see the Elephant
(Though all of them were blind),
That each by observation
Might satisfy his mind
The First approached the Elephant,
And happening to fall
Against his broad and sturdy side,
At once began to bawl:
“God bless me! But the Elephant
Is very like a wall!”
The Second, feeling of the tusk,
Cried, “Ho! What have we here?
So very round and smooth and sharp?
To me ’tis mighty clear
This wonder of an Elephant
Is very like a spear!”
The Third approached the animal,
And happening to take
The squirming trunk within his hands,
Thus boldly up and spake:
“I see,” quoth he, “the Elephant
Is very like a snake!”
The Fourth reached out an eager hand,
And felt about the knee.
“What most this wondrous beast is like
Is mighty plain,” quoth he;
“ ‘Tis clear enough the Elephant
Is very like a tree!”
The Fifth, who chanced to touch the ear,
Said: “E’en the blindest man
Can tell what this resembles most;
Deny the fact who can
This marvel of an Elephant
Is very like a fan!”
The Sixth no sooner had begun
About the beast to grope,
Than, seizing on the swinging tail
That fell within his scope,
“I see,” quoth he, “the Elephant
Is very like a rope!”
And so these men of Indostan
Disputed loud and long,
Each in his own opinion
Exceeding stiff and strong,
Though each was partly in the right,
And all were in the wrong!
Moral:
So oft in theologic wars,
The disputants, I ween,
Rail on in utter ignorance
Of what each other mean,
And prate about an Elephant
Not one of them has seen!
[1] Edited by corrector
[2] This paragraph is entirely built on the paper “OTSM axiom system” of Nikolai Khomenko (Khomenko, 2005) and discussions with him. Nevertheless, this document is not a word-for-word translation. When translating the paper we shall use the dictionary developed by NK and DK and translated in French by Ioulia Stein. Last version of the dictionary dates from 2002 and can be found at LGECO of INSA Strasbourg, France.
As the paper is not yet completely finished, some parts will be less developed than others. (I. Kaikov)
[3] Saxe, John Godfrey, (1963), "The Blind Men and the Elephant; John Godfrey Saxe's version of the famous Indian legend. Pictures by Paul Galdone," New York: Whittlesey House.
- 61417 reads


Recent comments
12 years 48 weeks ago
13 years 47 weeks ago
13 years 48 weeks ago
13 years 48 weeks ago